A konvekció alapjai II. - A hodográf használata
1. Bevezetés
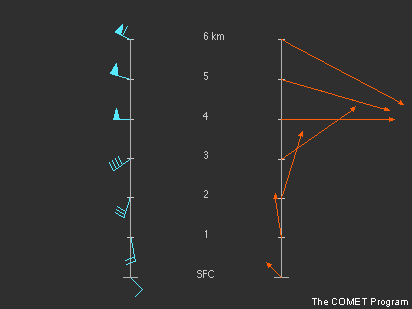
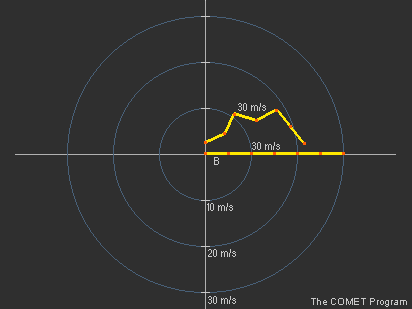
| A hodográf egy olyan grafikus eszköz, amelynek segítségével a vertikális szélnyírást tudjuk meghatározni. Konvektivitásra hajlamos időjárási helyzetekben a vertikális szélnyírás ismerete alapvetően fontos annak előrejelzéséhez, hogy milyen típusú zivatarra számíthatunk, hol keletkezhetnek új zivatarok, mekkora a szupercellák valószínűsége, ill. hogy hogyan alakul a zivatarok, zivatarrendszerek mozgása. A szimulált radarkép-animáción (1. ábra) eltérő szélnyírási feltételek között kifejlődő modellezett zivatarok sora látható, melyeken megfigyelhetjük, hogy a (bal alsó sarokban lévő) különböző hodográftípusokkal jellemzett vertikális szélnyírási profil hogyan befolyásolja a zivatarcellák megjelenési formáit. | ||||
|
||||
|
1.2 A hodográf |
||||
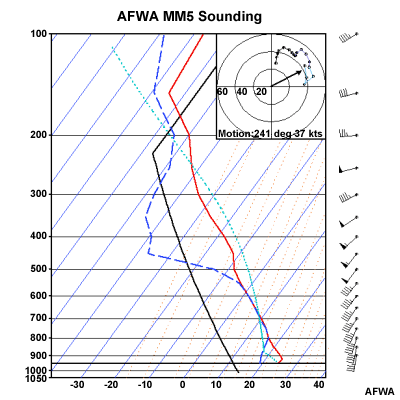
| Az adott zivatar környezetére vonatkozó helyes feltételezések pontosabb prognózist eredményeznek. A hodográf leírja számunkra a környezet szélnyírási viszonyait, amely jelentős hatással van a zivatarfelhők fejlődésére, felépítésére. Így tehát a szélnyírás és a felhajtóerő profiljának együttes figyelembevétele lényegesen jobb előrejelzést jelenthet. A 2. ábrán az AFWA MM5 modellezett rádiószondás felszállása látható, mellette a hozzá tartozó hodográffal. A kép forrása a Joint Army-Air Force Weather Information Network (JAAWIN) weboldal, de hasonló hodográfok/felszállási ábrák számtalan egyéb címen is elérhetőek. | ||||
|
||||
|
2. A hodográf ábrázolása
2.1 Szélzászlók, szélvektorok |
||||
| A rádiószondás felszállások vertikális szélprofilra vonatkozó adatainak hagyományos megjelenítési módja a szélzászlók használata, amelyekből leolvasható, hogy a különböző szinteken milyen szélirányok, milyen nagyságú szélsebességek vannak. A hodográf ezzel azonos információt közöl, mivel azonban ennek elsődleges célja a szélnyírás ábrázolása, ezért szélvektorok megjelenítésére van szükség. A szélzászlóval ellentétben a sebesség nagyságát a vektor hossza jelenti, nem pedig a jelölések különféle kombinációja. | ||||
|
||||
|
2.2 A polárkoordináta-rendszer |
||||
| A hodográf úgy áll elő, hogy a szélvektorokat egy polárkoordináta-rendszerbe helyezzük. A koordináta-rendszer tengelyei a négy égtájat adják meg. A vektorokat egy közös kezdőpontból, a tengelyek metszéspontjából, az origóból indítjuk, és úgy állítjuk be, hogy a szél mozgásának irányába mutassanak. A vektor hossza a sebesség nagyságát jelzi, az origó körüli koncentrikus körök pedig azonos nagyságú szélsebességeket jelentenek. A 4. ábrán látható hodográfon például 4 és 5 km-en is 25 m/s-os szeleket találunk, de míg az előbbi nyugatról fúj, addig az utóbbi nyugat-északnyugatról. | ||||
|
||||
| 2.3 A hodográf | ||||
| Jellemzően a koordináta-rendszerben nincsenek felrajzolva az adott magassági szintekhez tartozó szélvektorok, csak azok végpontjai. Ezek összekötésével jön létre maga a tulajdonképpeni hodográf. | ||||
|
||||
3. Vertikális szélnyírás
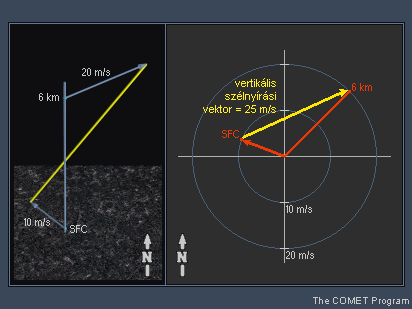
3.1 A vertikális szélnyírási vektor A vertikális szélnyírás a horizontális szélsebesség magassággal történő változását adja meg. A sebesség egy vektormennyiség, tehát nagysággal és iránnyal rendelkezik. Ily módon a vertikális szélnyírás két szint szélvektorának különbségeként határozható meg.
Az így kapott vektorkülönbséget vertikális szélnyírási vektornak nevezzük. Ennek nagyságát rendszerint m/s-ban írjuk fel az adott réteg vastagságával együtt (a 6. ábrán látható példában "25 m/s 6 km-en" v. "0-6 km-es szélnyírás 25 m/s"). Ha precízebben akarunk eljárni, akkor a szélnyírási vektor nagyságát a légréteg vastagságával osztva megkapjuk az egységnyi magasságkülönbségre eső szélnyírási értéket. A példa 25 m/s-os szélnyírását tehát 6000 m-rel (6 km-rel) osztva 0.004/s-os (0.004 1/s-os) érték adódik.
|
6. ábra Vertikális szélnyírás ábrázolása 6 km vastagságú légrétegben 3 dimenzóban és hodográf segítségével |
3.2 A vertikális szélnyírás megjelenítése A hodográf ideális eszköz a vertikális szélnyírás megjelenítéséhez. A polárkoordinátákat felhasználva az adott szintek közti szélnyírási vektort a szélvektorok végpontjait összekötő szakasz jelenti. A magassággal növekvő sorrendben meghúzott szakaszokból így rajzolódik ki a hodográf, melynek egy szegmense az adott légrétegben uralkodó vertikális szélnyírást mutatja.
Amennyiben a hodográf szélvektorai egymástól azonos távolságra lévő magassági szinteken helyezkednek el (általában km-enként vagy 500 m-enként), a nyírási vektorok könnyen összehasonlíthatóvá válnak. Ily módon a nyírási vektorok egymáshoz képesti hosszúsága rétegről rétegre megadja a szélnyírás relatív erősségét.
|
|
7. ábra A magassággal növekvő sorrendben meghúzott, a szélvektorok végpontjait összekötő szakaszokból kirajzolódik a hodográf |
3.3 Az egyes szintek közti szélnyírási vektor nagyságának megállapítása A vertikális szélnyírás teljes nagyságának ismerete fontos tényező a zivatarok struktúrájának és fejlődésének előrejelzésében, ezért lényeges, hogy valahogy ezt is meghatározzuk.
Ezt az egyes szélnyírási vektorok nagyságának becslésével kezdjük úgy, hogy a koordináta-rendszer tengelyének skálájához mérjük őket. Ezt megtehetjük ránézésre, de ha pontosabb végeredményt szeretnénk, vonalzóval is dolgozhatunk.
|
|
8. ábra Egy szélnyírási vektor nagyságának becslése |
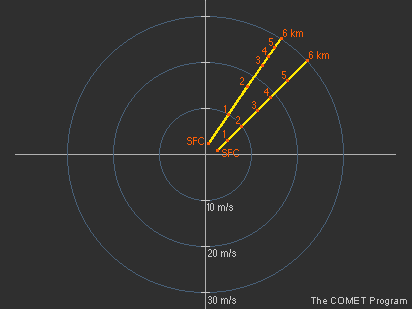
3.4 A teljes szélnyírás megállapítása A szélnyírási vektorok teljes hosszát (magát a teljes szélnyírást) úgy kapjuk meg, hogy egyszerűen összeadogatjuk azokat a részértékeket, amiket az egyes légrétegekhez tartozó nyírási vektorok nagyságának megbecslése/megmérése során kaptunk.
A 9. ábrán látható példánkban a teljes szélnyírás (minden egyes nyírási vektort figyelembe véve 0 és 6 km között) 60 m/s.
|
|
9. ábra A teljes szélnyírás, avagy a szélnyírási vektorok teljes hosszának megállapítása |
3.5 A szélnyírás nagyságának becslésével kapcsolatos nehézségek Előfordulhat, hogy a hodográf bonyolult alakja miatt a hossz szemmel történő becslése nehézségekbe ütközik, illetve nagy hibát okozhat. Ezekben az esetekben a pontosabb végeredmény érdekében érdemesebb inkább számítógépes programmal számolnunk.
|
10. ábra Egy görbült és egy egyenes hodográf, mindkettő ugyanakkora teljes szélnyírással |
3.6 A szélnyírás megoszlása a különböző szintek között Fontos azt is tanulmányoznunk a hodográfon, hogy a szélnyírás hogyan oszlik meg a különböző szintek között. Két azonos hosszúságú hodográf esetén egy olyan alapján, ahol alacsony szinten erős a szélnyírás, merőben más következtetést vonhatunk le a várható zivatarunk felépítésével, fejlődésével kapcsolatban, mint egy olyan alapján, ahol kicsi az alacsony szintű szélnyírás.
|
11. ábra Azonos hosszúságú, de eltérő eloszlású szélnyírással rendelkező egyenes hodográfok. Az egyiknél a talaj közelében koncentrálódik a szélnyírás, míg a másiknál egyenletesebb elrendeződés figyelhető meg. |
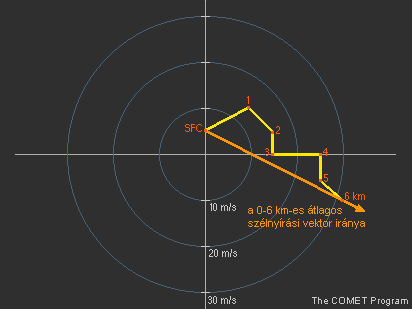
3.7 Az átlagos szélnyírási vektor Az átlagos szélnyírási vektor a zivatarok környezetének egy másik olyan fontos tulajdonsága, melyről szintén könnyebben kaphatunk képet hodográffal, mint egyéb adatok, eszközök segítségével. Az átlagos szélnyírási vektor iránya a szupercellák mozgásának előrejelzésében lehet segítségünkre.
Az átlagos szélnyírási vektor irányát (de nem a nagyságát) úgy határozhatjuk meg, hogy egyszerűen összekötjük a felszíni szelet jellemző koordinátát a 6 km-es szél koordinátájával. Azért az alsó 6 kilométeres légréteget vizsgáljuk, mert az befolyásolja leginkább a zivatarok fejlődését.
|
12. ábra Az átlagos szélnyírási vektor irányának meghatározása görbült hodográf esetén |
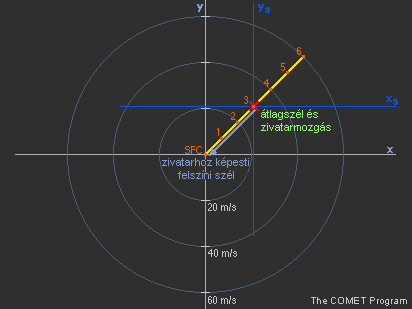
3.8 Az átlagos szélnyírási vektor kiszámítása Az átlagos szélnyírási vektor (nagyság és irány egyaránt) kiszámításának első lépése az egyes szélnyírási vektorok x és y koordinátáinak összeadása a 13. ábrán látható módon. Második lépésként a két kapott összeget elosztjuk a figyelembe vett szélnyírási vektorok számával (a példában 30/6=5, -15/6=-2.5). Az így létrejött két érték által meghatározott koordinátába fog mutatni az átlagos szélnyírási vektor. Ennek kezdőpontja a legalacsonyabb szintet, a felszíni szelet jellemző szélvektor végpontja (a képen: SFC), mely az eltolt koordináta-rendszer (x') origójaként szolgál (az y' az ábrán azért nincs külön feltüntetve, mert az jelen esetben megegyezik az eredeti y-tengellyel). Ha nem vagyunk kíváncsiak az átlagos szélnyírási vektor nagyságára, csak az irányára, elég az x és y komponensek összeadásával meghatározott pontba húznunk egy vonalat az eltolt koordináta-rendszer origójából. Az x/y arány (tehát az irány) nem változik az átlagolással, így nem meglepő, hogy a két módszer azonos irányú vektorokat eredményez.
Átlagolás nélkül az eljárás megegyezik az összes szélnyírási vektor összeadásával, ezért a legalacsonyabb és legmagasabb szintű szelet reprezentáló pont összekötése (a 3.7-es alfejezetben leírtaknak megfelelően) mindig egybeesik az átlagos szélnyírási vektor irányával.
Az eltolt koordináta-rendszer szerint (x') az átlagos szélnyírási vektor iránya délkelet felé mutat.
4. A hodográf alakja
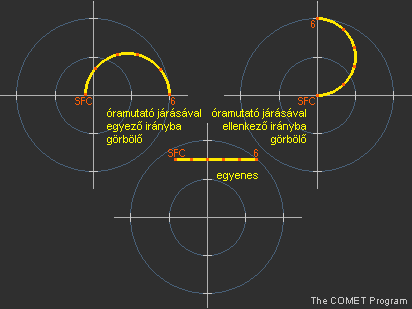
4.1 Egyenes vagy görbülő hodográf A szélnyírás nagyságán túl fontos ismernünk a hodográf alakját is, amely szintén nagymértékben befolyásolja a zivatarok fejlődését, struktúráját. Ennek tükrében kiemelhetőek a leglényegesebb kérdések. A hodográf viszonylag egyenes vagy inkább görbül? Ha görbül, melyik szinten jelentős a görbület, ill. a magassággal az óramutató járásával egyező vagy ellenkező irányú fordulást tapasztalunk?
|
14. ábra Egyenes és görbülő hodográf példák |
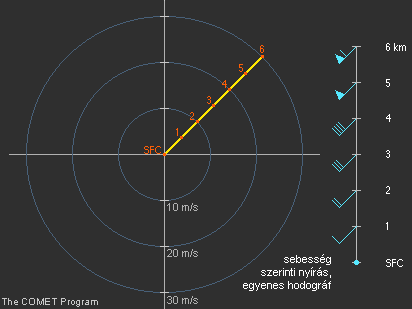
4.2 A sebesség szerinti ill. irány szerinti nyírás Tudjuk, hogy szélnyírás jön létre, ha a magassággal változik a szélsebesség (sebesség szerinti nyírás), ill. akkor is, ha a szél iránya változik (irány szerinti nyírás) a magasság függvényében. Azonban a szélnyírás típusának ilyen szempontok alapján történő vizsgálata nem sokat árul el a hodográf formájáról, mivel a szelek irányát és sebességét jellemzi, nem pedig a szélnyírási vektorokat.
Az mindenesetre igaz, hogy ha csak sebesség szerinti a szélnyírás, akkor egyenes hodográfot kapunk (egyirányú nyírás), a kizárólag irány szerinti nyírás pedig görbülő hodográfot eredményez (a magassággal fordul a nyírási vektor). Ezek kombinációja viszont bármilyen formájú elrendeződést kialakíthat.
Érdemes végignézni az ide tartozó ábrákat (15-18. ábra), melyeken a különböző szélnyírási típusok és hodográf-formák hasonlíthatóak össze.
|
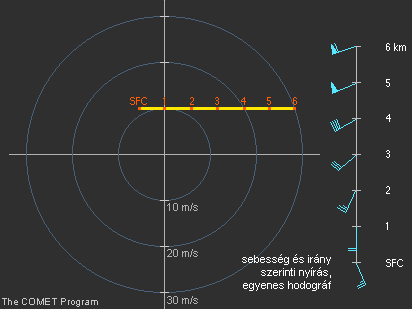
15. ábra Sebesség szerinti nyírás, egyenes hodográf |
|
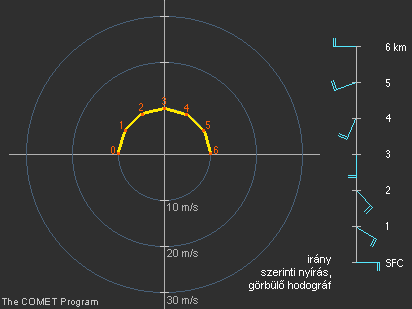
16. ábra Irány szerinti nyírás, görbülő hodográf |
|
17. ábra Sebesség és irány szerinti nyírás, egyenes hodográf |
|
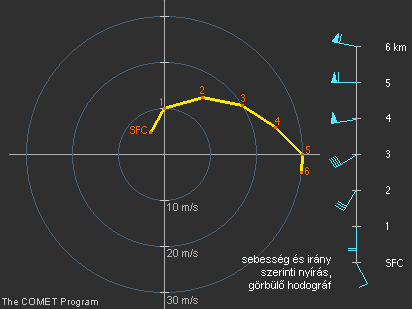
18. ábra Sebesség és irány szerinti nyírás, görbülő hodográf |
4.3 A hodográf és a nagyléptékű folyamatok Amíg az egymáshoz hasonló formájú hodográfok a zivatarok fejlődésére hasonló módon hatnak, addig a nagyobb skálájú folyamatokkal, ill. a várható konvektivitással kapcsolatban már egészen eltérő folyamatokra utalhatnak.
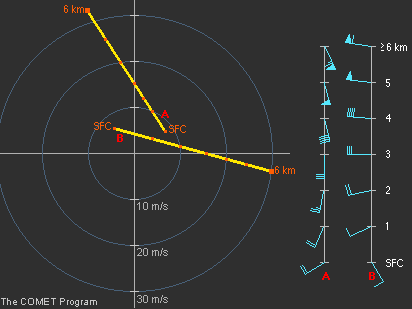
Példaképpen nézzük meg a 19. ábrán látható két egyenes hodográfot. Szignifikáns konvekció fellépésekor mindkettő olyan kettéváló szupercella kialakulását valószínűsíti, amikor a szétvált pár tagjai szimmetrikusan, tartósan fennmaradhatnak. Az "A" hodográf irány szerinti nyírása a magassággal az óramutató járásával ellenkező irányba forduló szeleket mutat (balra fordul a szél a magassággal), ami az adott légrétegben előforduló nagyléptékű hidegadvekcióra utal. A "B" hodográf viszont az óramutató járásával egyező irányú szélfordulást mutat (jobbra fordul a szél a magassággal), melegadvekciót jelezve. E két szélnyírási profil tehát egészen eltérő megvilágításba helyezi az egyéb környezeti tényezőktől függő lehetséges konvekciót. Emiatt a nagyléptékű viszonyokat nagyon fontos figyelembe venni a hodográf elemzésekor.
|
19. ábra Két egyenes, de eltérő nagyléptékű folyamatokra utaló hodográf összehasonlítása |
4.4 Gyakorlat - a hodográf ábrázolása
|
|
5. Zivatarmozgás és a zivatarhoz képesti szelek
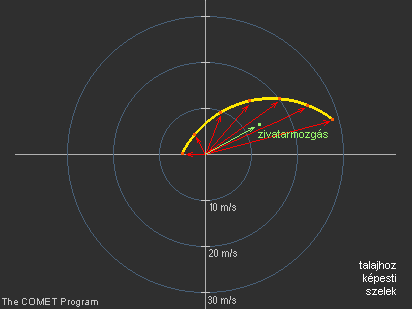
5.1 Talajhoz viszonyított szelek és a zivatarhoz képesti szelek A zivatar fejlődésének előrejelzésekor nem csak annak jelenlegi környezetére kell tekintettel lennünk, hanem a zivatar mozgása révén a jövőbeni környezetére is. Egy zivatar alakulására pl. hatással van a beáramlást alkotó levegő jellege.
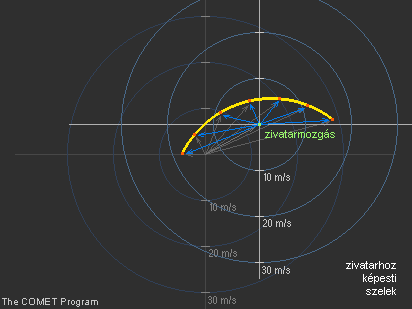
A zivatarhoz képesti szélsebesség jobb megértéséhez először meg kell határoznunk vagy becsülnünk a zivatar mozgását a hodográfon (ez egyaránt lehet előrejelzett érték vagy egy már létező zivatar megfigyelt sebessége). Ezután már módunkban áll tanulmányozni, hogy a zivatarhoz képest milyen szélviszonyok uralkodhatnak. Mivel a zivatar mozog a környezetében, gyakran nagy különbségek adódnak a felszín egy adott pontjához viszonyított, rádiószondás felszállás alapján megállapított szélprofil, ill. a zivatarhoz képesti szélprofil között. A különbségeket az alábbi két ábrán (20., 21. ábra) látható hodográfon is jól megfigyelhetjük.
|
20. ábra Hodográf a talajhoz képesti szélvektorokkal |
|
21. ábra Hodográf a zivatarhoz képesti szélvektorokkal |
A zivatarhoz képesti szelek meghatározását azzal kezdjük, hogy a koordináta-rendszert eltoljuk a zivatarmozgás vektorának végpontjába, tehát ide kerül az origó. Így a zivatarmozgás tulajdonképpen 0 lesz. Ebből a pontból aztán újraszámoljuk a környezeti szeleket. Más megközelítésben ugyanezt eredményezi, ha a zivatar talajhoz viszonyított mozgásvektorát minden egyes szint talajhoz viszonyított szélvektorából kivonjuk. Egyszerűbben megfogalmazva a zivatarmozgáshoz képesti szélsebességeket úgy állapítjuk meg, hogy a zivatarmozgás koordinátáját összekötjük az egyes szintek koordinátáival. Egy ilyen vektor tulajdonképpen a zivatar mozgásának sebessége és a környezet adott szintjének szélsebessége közti különbséget adja meg. 5.2 A zivatar mozgásának meghatározása A zivatarhoz képesti szélsebesség tanulmányozásához először a zivatar mozgását kell meghatároznunk. Egy már meglévő zivatar esetében a radarképek vagy műholdképek léptetésével ez könnyen megoldható. Azonban ha a zivatar mozgása még nem egyértelműen látható, vagy még ki sem alakult a zivatar, akkor a mozgást csak becsülni tudjuk valamilyen módszer segítségével.
Feltehetjük, hogy a legtöbb zivatar - legalábbis kezdeti stádiumban - nagyjából a vertikális kiterjedésének megfelelő rétegvastagságban fújó szelek átlagával mozog. Mivel a megfigyelések és a számítógépes modellek eredményei egyaránt arra utalnak, hogy a zivatarmozgás az alacsonyabb szintek szeleire a legérzékenyebb, az átlagszelet a 0-tól 6 km-ig terjedő légréteg szélviszonyai alapján számoljuk. A szupercellák mozgása rendszerint eltér az átlagszéltől, ezt azonban egy másik ismeretterjesztő anyagban ("A konvekció alapjai III. - A szélnyírás és a konvekció kapcsolata") fejtjük ki részletesen.
Léteznek különféle szoftvercsomagok (mint pl. a SHARP), melyek automatikusan kiszámítják az átlagszelet, azonban nem árt ismernünk, hogy ez a művelet ténylegesen hogyan is történik.
|
22. ábra Az átlagszél meghatározása egyenes hodográf esetén |
5.3 A zivatarmozgás becslése egyenes hodográf esetén Viszonylag egyenes hodográf esetén az átlagszél becslése egyszerű, mivel az ilyenkor közelítőleg a 0-6 km-es hodográf-szakasz felezőpontjára esik. Az egyes szintek zivatarhoz képesti szélviszonyait a már korábban leírt módon számítjuk. A koordináta-rendszer eltolásával (xs, ys) a zivatarmozgás nullára redukálódik, a zivatarhoz képesti szelet pedig úgy kapjuk meg, hogy egy adott szint szélsebességéhez ebből az új origóból húzunk egy vektort.
A pontosabb végeredmény érdekében súlyozottan is figyelembe vehetnénk az alacsonyabb szintek szeleit. A légkör ezen része ugyanis a nagyobb sűrűség miatt nagyobb momentummal járul hozzá a zivatar mozgásához. Ez azonban csak jelentéktelen különbséget eredményezne az eredeti, egyszerű átlaghoz képest, ezért az utóbbit használjuk a továbbiakban is. Emellett az eltérés nagyrészt azzal magyarázható, hogy csak a 0 és 6 km közti szelekkel számolunk.
|
23. ábra Az átlagszél és a zivatarmozgás meghatározása egyenes hodográf esetén |
5.4 A zivatarmozgás becslése görbülő hodográf esetén Amikor a hodográf görbül, már egy kicsit komplikáltabbá válik a művelet. Meg kell néznünk közelebbről, valójában hogyan is történik az átlagszél kiszámítása ahelyett, hogy egy hozzávetőleges eljárást alkalmaznánk.
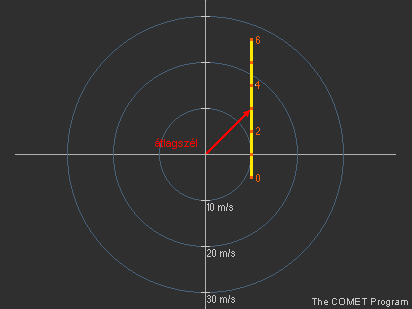
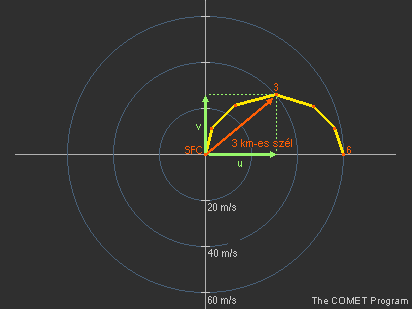
Mindegyik szélvektor leírható szétválasztott u és v komponensek segítségével, tehát a szélvektorokat szintenként felbontjuk a sebesség u és v komponenseire. A 24. ábrán lévő példában a 3 km-es szint szélvektorának felbontása látható.
Az átlagszél kiszámításához először külön átlagoljuk az u és külön a v komponenseket (a meghatározott - rendszerint a 0-6 km-es - légréteg összes szintjét figyelembe véve), majd az így létrejött átlagos u és v vektort összeadva megkapjuk a kívánt koordinátákat. A gyakorlatban ez nem túl gyors eljárás, azonban a hodográf szerencsére lehetővé teszi a vizuális elemzést.
|
24. ábra Egy adott szélvektor u és v komponensének meghatározása |
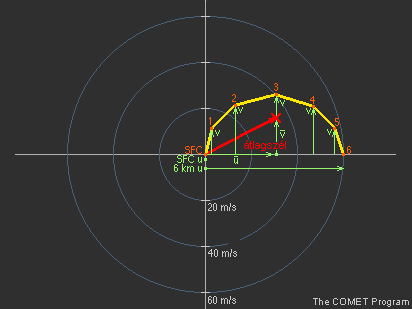
5.5 A zivatarmozgás becslésének lépései görbülő hodográf esetén Az átlagszél számításának bemutatásához térjünk vissza a görbülő hodográfos példánkhoz (25. ábra). Láthatjuk, hogy a hodográf minden pontja rendelkezik egy u és egy v komponenssel. Az átlagszél u összetevőjének megállapításához elég csak a felszíni (0 km-es) és a 6 km-es szelet figyelembe venni. Ez a szelek eléggé egyenletes elrendeződését feltételezi a hodográf mentén, de egy durva becslésnek megfelel. A következő lépés az összes szint v komponenseinek átlagolása. Az így kapott átlagos u és v vektor összeadása az átlagszél sebességének jó becslését eredményezi.
|
25. ábra Az átlagszél és a zivatarmozgás meghatározása görbülő hodográf esetén |
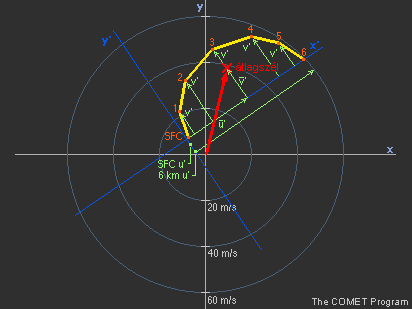
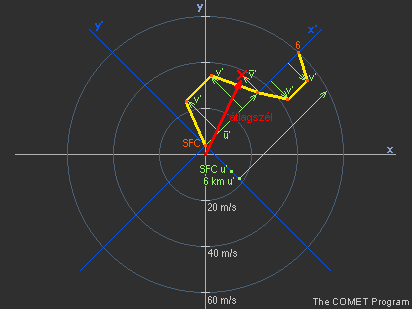
Ez a technika bármilyen irányítottságú hodográf esetén alkalmazható (26. ábra), de ilyenkor előbb el kell tolnunk az x-y koordináta-rendszert úgy, hogy a felszíni (0 km-es) szélvektor végpontjába helyezzük az origót. Ezt követően az x'-y'-tengelyeket úgy kell elforgatnunk, hogy az x' átmenjen a 6 km-es szélnek megfelelő ponton. Ezután az előzőekben már leírtak alapján folytatjuk tovább az átlagszél becslését.
|
26. ábra Az átlagszél és a zivatarmozgás meghatározása tetszőleges irányítottságú görbülő hodográf esetén |
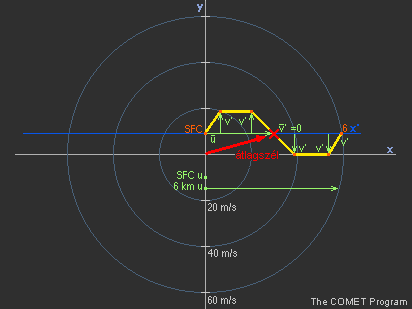
5.6 A zivatarmozgás becslése többszörösen görbülő hodográf esetén Amint az alábbi példák (27., 28. ábra) is mutatják, ez a módszer akkor is segíthet az átlagszél meghatározásában, ha a hodográf a többszörös görbületek bonyolultabb kombinációjából áll. Mindössze kicsit komolyabb munkát igényel az átlagszél v komponensének kielégítő becslése, ha a hodográf formája még csak nem is szimmetrikus.
|
27. ábra Az átlagszél és a zivatarmozgás meghatározása bonyolult hodográf esetén |
|
28. ábra Az átlagszél és a zivatarmozgás meghatározása tetszőleges irányítottságú bonyolult hodográf esetén |
5.7 Gyakorlat - a zivatarhoz képesti felszíni szél meghatározása
|
|
6. Összefoglalás
Ebből az ismeretterjesztő anyagból különféle szélnyírási paraméterek kiszámítását tanulhattuk meg, ill. röviden megnézhettük azok használatát (az alábbi listában a lényegi elemek vannak röviden kiemelve). Azzal, hogy hogyan befolyásolja a szélnyírás a zivatarokat, "A konvekció alapjai III. - A szélnyírás és a konvekció kapcsolata" című anyagban foglalkozunk részletesen.
| — | A hodográf elsődleges célja a vertikális szélnyírás megjelenítése, ábrázolása | |
| — | A vertikális szélnyírás azt mutatja meg, hogy a horizontális szélsebesség hogyan változik a magassággal. Meghatározása úgy történik, hogy vesszük a légkör két szintjének horizontális szélsebesség-vektorait, és megállapítjuk az ezek közötti vektoriális különbséget | |
| — | A hodográf nem szélzászlókon, hanem szélvektorokon alapul, és úgy készítjük el, hogy a szélvektorokat egy polárkoordináta-rendszer közös kezdőpontjába tesszük, majd a végpontjaikat összekötjük | |
| — | Egy bizonyos légréteg teljes szélnyírási nagysága fontos tényező a zivatarok lehetséges felépítésének, fejlődésének előrejelzésében. Ha vesszük a vizsgált légréteg összes szélnyírási vektorát, majd ezek hosszát (nagyságát) sorra összeadogatjuk, akkor végül megkapjuk a teljes szélnyírási nagyságot | |
| — | Az átlagos szélnyírási vektor irányát (de nem a nagyságát) úgy állapítjuk meg, hogy a felszíni (0 km-es) szelet jelző pontot összekötjük a 6 km-es szelet reprezentáló ponttal | |
| — | Az átlagos szélnyírási vektort (irányát és nagyságát együtt) egyszerű kiszámítani, csupán minden egyes szélnyírási vektort figyelembe véve azok x és y komponenseit kell átlagolnunk | |
| — | A szélnyírás nagyságán kívül azzal is foglalkozunk, hogy a hodográf viszonylag egyenes, vagy inkább görbülő formát mutat. Emellett amíg az egymáshoz hasonló alakú hodográfok a zivatarok fejlődésére hasonló módon hatnak, addig a nagyobb skálájú folyamatokkal, ill. a várható konvektivitással kapcsolatban már egészen eltérő folyamatokra utalhatnak | |
| — | Mivel a zivatar mozog a környezetében, gyakran nagy különbségek adódnak a felszín egy adott pontjához viszonyított, rádiószondás felszállás alapján megállapított szélprofil, ill. a zivatarhoz képesti szélprofil között. A zivatarhoz képesti szelek szintén kiszámíthatóak a hodográf alapján | |
| eredeti forrás: | |
| — | Principles of Convection II: Using Hodographs |
| — | COMET program |
| — | Molnár "Storman" Ákos |
| — | Polyánszky "Meteorman" Zoltán |
- A hozzászóláshoz belépés szükséges